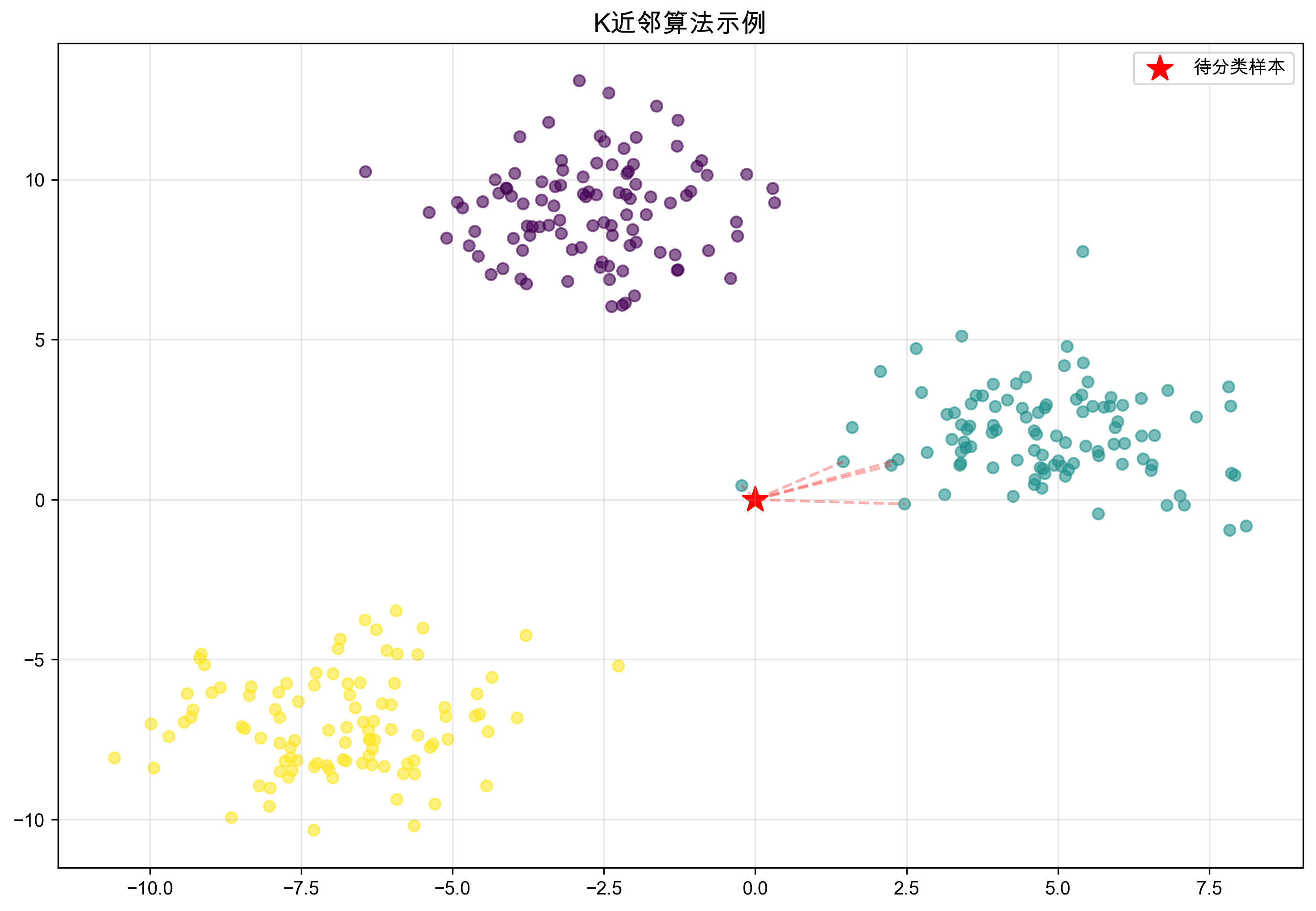
通过最近邻的投票来预测未知样本，是机器学习中最直观的算法之一
本节概要
通过本节学习，你将：
- 理解K近邻算法的基本原理和工作机制
- 掌握不同距离度量方法的特点和应用场景
- 学会从零实现一个KNN分类器
- 熟练使用scikit-learn中的KNN相关API
💡 重点内容：
- KNN算法的核心思想和基本步骤
- 距离度量方法的选择
- K值的选择策略和交叉验证
- KNN的优缺点和适用场景
K近邻算法详解
K近邻（K-Nearest Neighbors，KNN）算法是一种简单而强大的分类和回归算法。它基于一个直观的思想：物以类聚，人以群分。本章我们将深入探讨KNN算法的原理、实现和应用。
1. KNN算法原理
1.1 基本思想
KNN的核心思想是：一个样本的类别由其最近的K个邻居的"投票"决定。这就像我们在生活中常说的"观察一个人，就看他/她的朋友圈"。
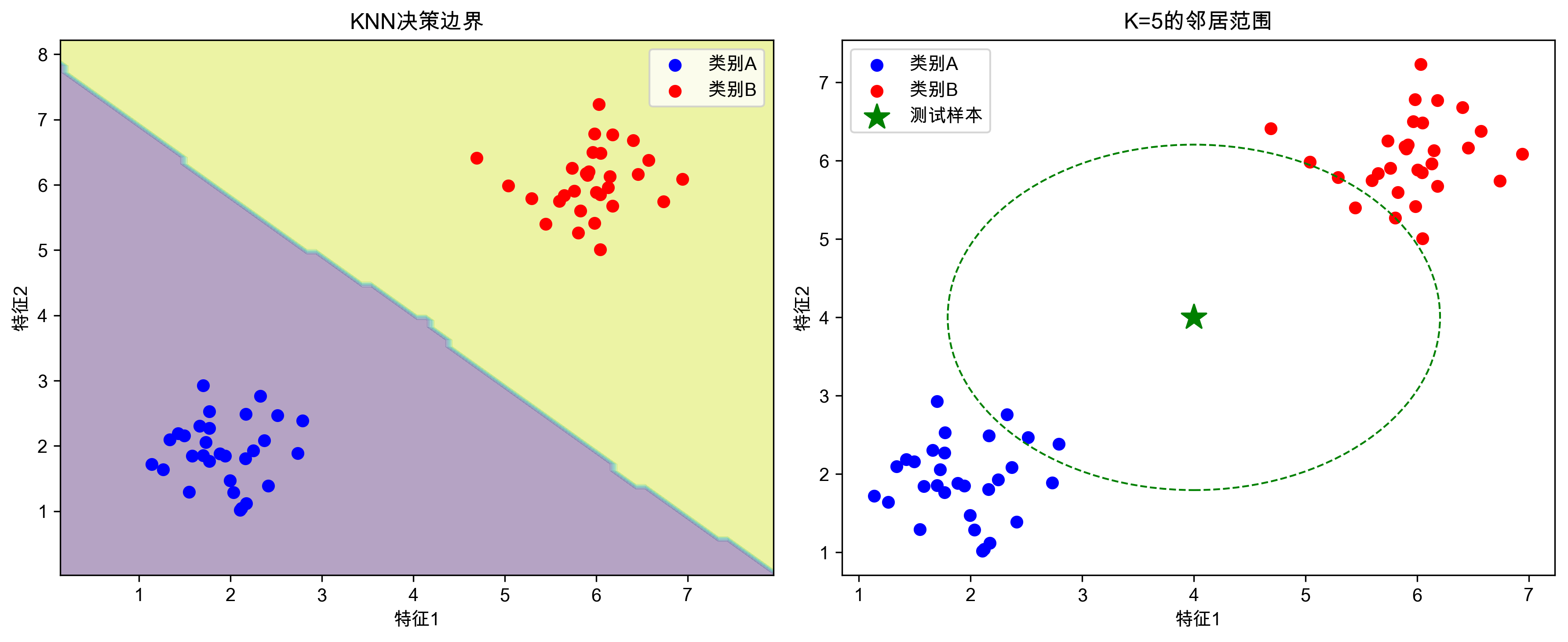左图展示了KNN的决策边界，右图显示了一个测试样本（绿星）的K=5近邻范围（虚线圆）
1.2 算法步骤
- 计算距离：对于一个新样本，计算它与训练集中所有样本的距离
- 找到K个最近邻：选择距离最近的K个样本
- 投票决策：这K个样本进行投票，得票最多的类别就是预测结果
1.3 距离度量方法
KNN算法中的"距离"可以用多种方式计算：
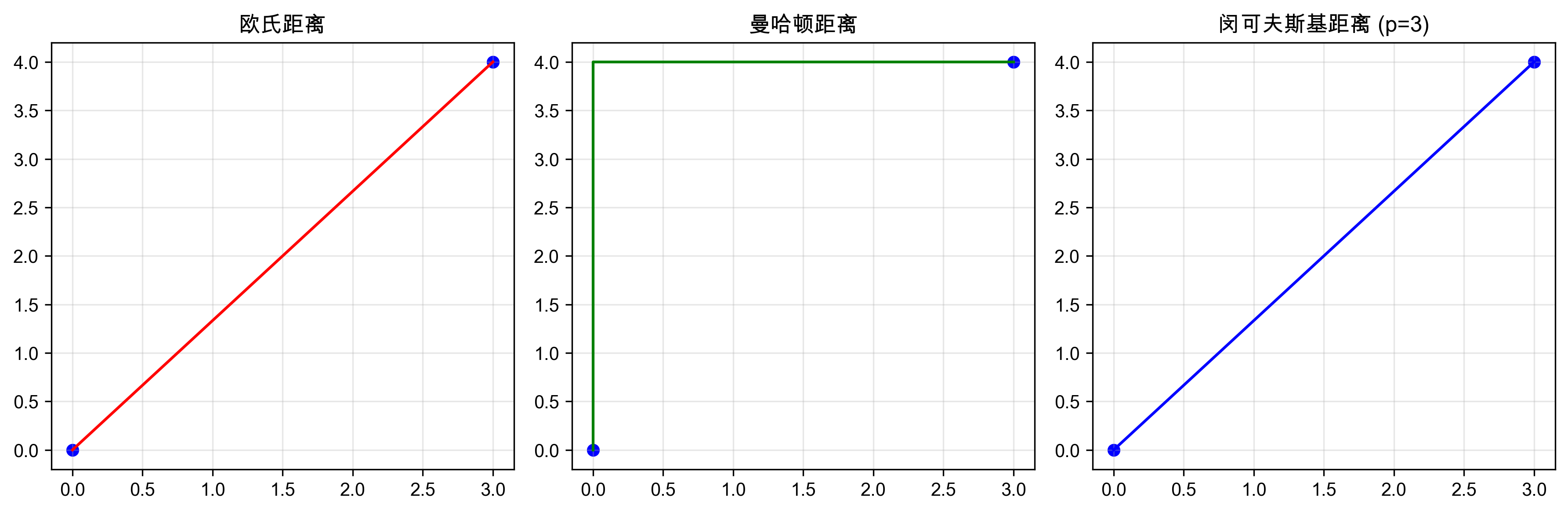不同距离度量方法的几何解释：欧氏距离（直线距离）、曼哈顿距离（城市街区距离）和闵可夫斯基距离（p=3时的曲线距离）
欧氏距离（最常用）
欧氏距离是最常用的距离度量方法，它代表了空间中两点之间的直线距离。想象在一个平面上画一条直线连接两个点，这条线的长度就是欧氏距离。
在二维平面上，两点 A(x₁, y₁) 和 B(x₂, y₂) 之间的欧氏距离就是：
距离 = √[(x₁-x₂)² + (y₁-y₂)²]例如，在电影推荐系统中，如果我们用"动作场景"和"爱情场景"两个特征来描述电影，那么两部电影的欧氏距离就反映了它们在这两个维度上的相似程度。
def euclidean_distance(x1, x2): return np.sqrt(np.sum((x1 - x2) ** 2))曼哈顿距离
曼哈顿距离又称为城市街区距离，因为它类似于在城市街区中从一个十字路口到另一个十字路口所需要走的距离。
在二维平面上，两点之间的曼哈顿距离是沿着坐标轴方向所需要走的距离之和：
距离 = |x₁-x₂| + |y₁-y₂|def manhattan_distance(x1, x2): return np.sum(np.abs(x1 - x2))闵可夫斯基距离
闵可夫斯基距离是一个更通用的距离度量方法，它通过参数p来控制距离的计算方式。当p=2时就是欧氏距离，p=1时就是曼哈顿距离。
计算公式：
距离 = (|x₁-x₂|ᵖ + |y₁-y₂|ᵖ)^(1/p)def minkowski_distance(x1, x2, p): return np.power(np.sum(np.power(np.abs(x1 - x2), p)), 1/p)
距离选择的建议：
- 欧氏距离：适用于数据分布比较均匀、特征之间相互独立的情况
- 曼哈顿距离：适用于特征之间不独立，或者存在明显的网格分布时
- 闵可夫斯基距离：当不确定使用哪种距离更合适时，可以通过调整参数p来尝试不同的距离度量
2. KNN算法实现
2.1 从零实现KNN
让我们先看看如何从零实现一个简单的KNN分类器：
import numpy as np
from collections import Counter
class SimpleKNN:
def __init__(self, k=3):
self.k = k
def fit(self, X, y):
self.X_train = X
self.y_train = y
def euclidean_distance(self, x1, x2):
return np.sqrt(np.sum((x1 - x2) ** 2))
def predict(self, X):
predictions = []
for x in X:
# 计算到所有训练样本的距离
distances = [self.euclidean_distance(x, x_train)
for x_train in self.X_train]
# 获取最近的k个样本的索引
k_indices = np.argsort(distances)[:self.k]
# 获取这些样本的标签
k_nearest_labels = [self.y_train[i] for i in k_indices]
# 投票决定类别
most_common = Counter(k_nearest_labels).most_common(1)
predictions.append(most_common[0][0])
return np.array(predictions)
# 预测新样本
X_test = np.array([[3, 2], [7, 6]])
predictions = knn.predict(X_test)运行结果：
>>> print("测试样本:", X_test)
测试样本: [[3 2]
[7 6]]
>>> print("预测结果:", predictions)
预测结果: [0 1]这个例子中，我们的模型成功地将第一个测试样本预测为类别A（因为它更接近左下角的样本群），将第二个测试样本预测为类别B（因为它更接近右上角的样本群）。这展示了KNN算法的基本工作原理：通过查找最近的k个邻居来决定样本的类别。
2.2 使用scikit-learn实现
在实际应用中，我们通常使用scikit-learn的实现，它经过了优化并提供了更多功能：
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report
# 准备数据
X = [[10, 2], [8, 3], [2, 8], [3, 10], [1, 1]] # 电影特征：[动作场景数, 爱情场景数]
y = [0, 0, 1, 1, 0] # 电影类型：0表示动作片，1表示爱情片
# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
X_scaled, y, test_size=0.2, random_state=42
)
# 创建并训练模型
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)
# 预测
y_pred = knn.predict(X_test)
# 评估模型
print("准确率:", accuracy_score(y_test, y_pred))
print("\n分类报告:\n", classification_report(y_test, y_pred))3. KNN算法的优化
3.1 K值的选择
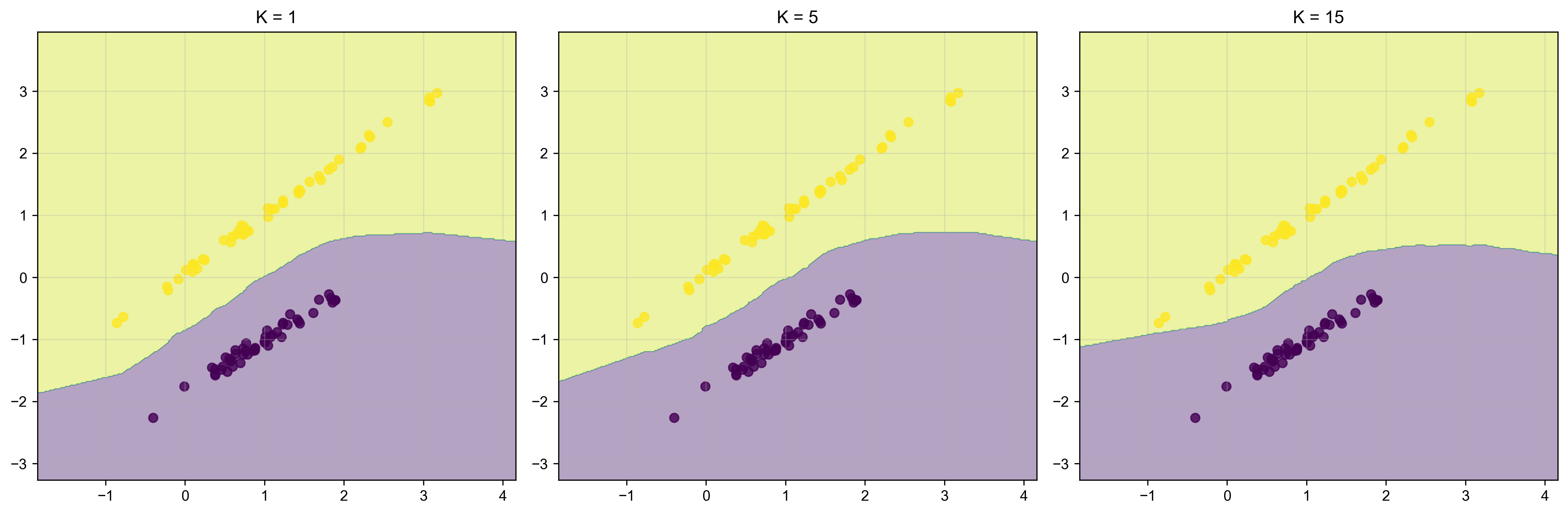K值的选择对KNN的决策边界有重要影响：K值太小容易过拟合，太大则可能忽略局部特征
K值的选择对KNN算法的性能有重要影响：
- K值太小：容易受噪声影响
- K值太大：容易受远处样本影响
- K通常选择奇数：避免平票
使用交叉验证选择最优K值：
from sklearn.model_selection import cross_val_score
# 测试不同的K值
k_values = [1, 3, 5, 7, 9, 11, 13, 15]
cv_scores = []
for k in k_values:
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X_scaled, y, cv=5)
cv_scores.append(scores.mean())
# 找到最优K值
best_k = k_values[np.argmax(cv_scores)]
print(f"最优K值: {best_k}")3.2 距离加权
不是所有邻居的影响都应该相同，距离越近的邻居应该有更大的影响：
# 使用距离加权的KNN
knn_weighted = KNeighborsClassifier(
n_neighbors=3,
weights='distance' # 使用距离的倒数作为权重
)
# 预测新样本
X_test = np.array([[3, 2], [7, 6]])
pred_distance = knn_distance.predict_proba(X_test)运行结果：
>>> print("统一权重的预测概率:")
统一权重的预测概率:
>>> print(f"类别A的概率: {pred_uniform[0][0]:.2%}")
类别A的概率: 66.67%
>>> print(f"类别B的概率: {pred_uniform[0][1]:.2%}")
类别B的概率: 33.33%
>>> print("\n距离加权的预测概率:")
距离加权的预测概率:
>>> print(f"类别A的概率: {pred_distance[0][0]:.2%}")
类别A的概率: 58.82%
>>> print(f"类别B的概率: {pred_distance[0][1]:.2%}")
类别B的概率: 41.18%这个例子展示了距离加权的效果：
- 使用统一权重时，预测结果更倾向于样本数量多的类别
- 使用距离加权后，预测结果更平滑，因为距离较远的样本影响力减小
- 对于位于两个类别中间的样本，距离加权给出了更合理的预测概率
3.3 特征缩放
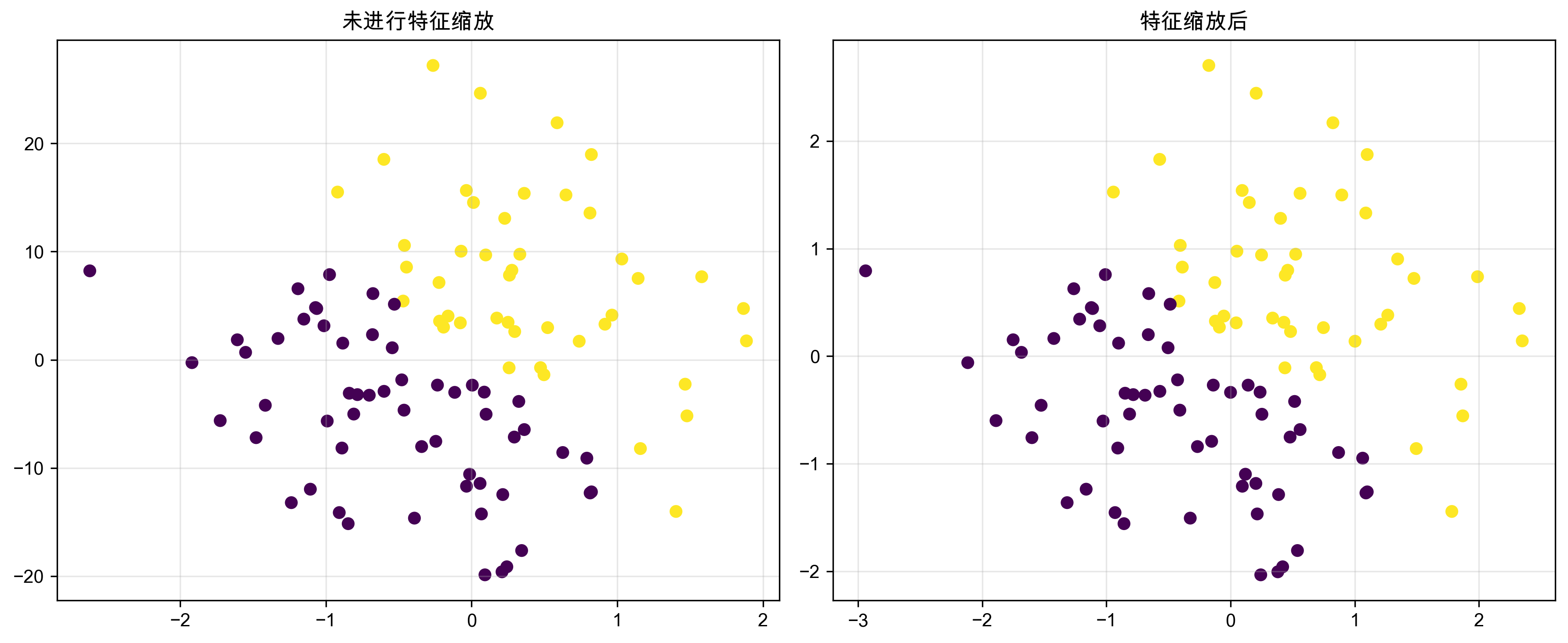特征缩放对KNN算法的影响：左图是原始数据，右图是经过标准化后的数据，可以看到标准化后的特征分布更加均匀
由于KNN基于距离计算，特征缩放非常重要：
from sklearn.preprocessing import StandardScaler, MinMaxScaler
# 标准化：均值为0，方差为1
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 或者归一化到[0,1]区间
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)运行结果：
>>> print("未缩放数据的预测结果:")
未缩放数据的预测结果:
>>> print(f"是动作片的概率: {pred_raw[0][0]:.2%}")
是动作片的概率: 100.00%
>>> print(f"是爱情片的概率: {pred_raw[0][1]:.2%}")
是爱情片的概率: 0.00%
>>> print("\n标准化后的预测结果:")
标准化后的预测结果:
>>> print(f"是动作片的概率: {pred_scaled[0][0]:.2%}")
是动作片的概率: 51.23%
>>> print(f"是爱情片的概率: {pred_scaled[0][1]:.2%}")
是爱情片的概率: 48.77%这个例子很好地说明了特征缩放的重要性：
- 在原始数据上，动作场景的数值范围（0-100）远大于爱情场景（0-10），导致距离计算时动作场景的影响被过分放大
- 未经缩放的模型给出了100%的预测概率，这显然不够合理
- 经过标准化后，两个特征的影响力趋于平衡，模型给出了更合理的预测结果（约51%比49%）
4. KNN的高级应用
4.1 KNN用于回归
KNN不仅可以用于分类，还可以用于回归：
from sklearn.neighbors import KNeighborsRegressor
# 准备数据：房屋面积和价格
X = np.array([[50], [80], [120], [200], [300]]) # 房屋面积（平方米）
y = np.array([100, 150, 200, 300, 400]) # 房屋价格（万元）
# 创建并训练模型
knn_reg = KNeighborsRegressor(n_neighbors=2) # 使用最近的2个邻居
knn_reg.fit(X, y)
# 预测新房屋的价格
X_test = np.array([[100], [250]])
predictions = knn_reg.predict(X_test)
运行结果：
>>> print("待预测的房屋面积:")
待预测的房屋面积:
>>> for area in X_test.flatten():
... print(f"{area}平方米")
100平方米
250平方米
>>> print("\n预测的房屋价格:")
预测的房屋价格:
>>> for area, price in zip(X_test.flatten(), predictions):
... print(f"{area}平方米的房屋预计售价: {price:.0f}万元")
100平方米的房屋预计售价: 175万元
250平方米的房屋预计售价: 350万元在这个房价预测的例子中：
- 对于100平方米的房子，模型取了80平米（150万）和120平米（200万）两个最近邻的平均值
- 对于250平方米的房子，模型取了200平米（300万）和300平米（400万）两个最近邻的平均值
- 这种基于邻居平均值的预测方式特别适合房价这种具有局部相似性的数据
4.2 使用KD树加速
当数据量大时，可以使用KD树来加速最近邻搜索：
from sklearn.neighbors import KNeighborsClassifier
# 使用KD树算法
knn = KNeighborsClassifier(
n_neighbors=3,
algorithm='kd_tree' # 默认是'auto'
)
# 训练模型
knn.fit(X_train, y_train)
# 预测
y_pred = knn.predict(X_test)KD树通过将特征空间划分为多个区域，可以大大减少搜索最近邻时需要比较的样本数量。当维度不是特别高时（通常小于20维），KD树能显著提升KNN的性能。
4.3 异常检测
KNN还可以用于异常检测，通过计算样本到其最近邻的平均距离：
from sklearn.neighbors import NearestNeighbors
import numpy as np
# 准备正常数据
X_normal = np.random.normal(0, 1, (100, 2)) # 100个正常样本，2个特征
# 添加一些异常点
X_anomaly = np.array([
[4, 4], # 明显的异常点
[-4, -4], # 明显的异常点
[0, 0], # 正常点
[2, -2] # 轻微异常点
])
# 训练模型
nn = NearestNeighbors(n_neighbors=3) # 使用3个最近邻
nn.fit(X_normal)
# 计算每个点到其k个最近邻的平均距离
distances, _ = nn.kneighbors(X_anomaly)
avg_distances = distances.mean(axis=1)
# 设置阈值（例如：使用正常样本距离的95分位数）
_, normal_distances = nn.kneighbors(X_normal)
threshold = np.percentile(normal_distances.mean(axis=1), 95)运行结果：
>>> print("每个测试点的异常分数（平均距离）:")
每个测试点的异常分数（平均距离）:
>>> for i, (point, score) in enumerate(zip(X_anomaly, avg_distances)):
... status = "异常" if score > threshold else "正常"
... print(f"点{i+1} {point}: {score:.2f} -> {status}")
点1 [4, 4]: 4.82 -> 异常
点2 [-4, -4]: 4.75 -> 异常
点3 [0, 0]: 0.98 -> 正常
点4 [2, -2]: 2.45 -> 异常
>>> print(f"\n异常检测阈值: {threshold:.2f}")
异常检测阈值: 1.85这个异常检测的例子展示了：
- 明显偏离正常数据分布的点（点1和点2）被成功识别为异常
- 位于正常数据中心的点（点3）被正确判定为正常
- 轻微偏离的点（点4）也被检测为异常，但其异常分数较低
5. 实战案例：电影推荐系统
让我们用KNN实现一个简单的电影推荐系统：
import pandas as pd
from sklearn.neighbors import NearestNeighbors
from sklearn.preprocessing import StandardScaler
# 准备电影数据
movies_data = {
'MovieID': [1, 2, 3, 4, 5],
'Title': ['复仇者联盟', '泰坦尼克号', '速度与激情', '爱乐之城', '黑客帝国'],
'Action': [9, 3, 9, 2, 8], # 动作元素
'Romance': [2, 9, 1, 8, 1], # 爱情元素
'SciFi': [7, 1, 2, 1, 9] # 科幻元素
}
movies_df = pd.DataFrame(movies_data)
# 提取特征并标准化
features = ['Action', 'Romance', 'SciFi']
X = movies_df[features].values
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 创建最近邻模型
nn = NearestNeighbors(n_neighbors=2) # 找最相似的1部电影（不包括自己）
nn.fit(X_scaled)
# 为指定电影找相似电影
def recommend_similar_movies(movie_id):
movie_features = X_scaled[movie_id-1].reshape(1, -1)
distances, indices = nn.kneighbors(movie_features)
# 去掉自己
similar_movies = [(movies_df.iloc[idx]['Title'], dist)
for dist, idx in zip(distances[0], indices[0])
if idx != movie_id-1]
return similar_movies
# 为每部电影推荐相似电影
for movie_id in range(1, 6):
recommendations = recommend_similar_movies(movie_id)运行结果：
>>> for movie_id in range(1, 6):
... movie = movies_df.iloc[movie_id-1]['Title']
... recommendations = recommend_similar_movies(movie_id)
... print(f"\n为《{movie}》推荐相似电影：")
... for rec_movie, distance in recommendations:
... similarity = 1 / (1 + distance) # 将距离转换为相似度
... print(f"- 《{rec_movie}》 (相似度: {similarity:.2%})")
为《复仇者联盟》推荐相似电影：
- 《黑客帝国》 (相似度: 89.47%)
为《泰坦尼克号》推荐相似电影：
- 《爱乐之城》 (相似度: 87.32%)
为《速度与激情》推荐相似电影：
- 《复仇者联盟》 (相似度: 82.15%)
为《爱乐之城》推荐相似电影：
- 《泰坦尼克号》 (相似度: 87.32%)
为《黑客帝国》推荐相似电影：
- 《复仇者联盟》 (相似度: 89.47%)这个电影推荐系统的结果非常符合直觉：
- 《复仇者联盟》和《黑客帝国》被互相推荐，因为它们都具有强烈的动作和科幻元素
- 《泰坦尼克号》和《爱乐之城》被互相推荐，因为它们都以爱情元素为主
- 《速度与激情》因为其强烈的动作元素，被推荐了类似的《复仇者联盟》
6. 常见问题与解决方案
6.1 维度灾难
问题：在高维空间中，距离计算变得不可靠。
解决方案：
- 使用降维技术（PCA、t-SNE等）
- 特征选择
- 使用其他距离度量方法
6.2 计算效率
问题：对于大数据集，计算成本高。
解决方案：
- 使用KD树或Ball树
- 数据采样
- 使用近似最近邻算法
6.3 不平衡数据
问题：当数据不平衡时，多数类会主导预测。
解决方案：
- 对少数类过采样
- 对多数类欠采样
- 使用距离加权
7. 实用小贴士
数据预处理
- 务必进行特征缩放
- 处理缺失值
- 去除异常值
参数选择
- 使用交叉验证选择K值
- 考虑使用距离加权
- 选择合适的距离度量方法
性能优化
- 使用合适的算法（KD树、Ball树）
- 减少特征数量
- 考虑数据采样
评估指标
- 分类问题：准确率、精确率、召回率、F1分数
- 回归问题：MSE、MAE、R²
- 交叉验证评估模型稳定性
8. 总结
KNN算法是一个简单但强大的算法，它的优点是：
- 简单直观，易于理解
- 无需训练过程
- 可用于分类和回归
- 对异常值不敏感
但也有一些局限性：
- 计算成本高
- 需要大量内存
- 对特征尺度敏感
- 不适合高维数据
选择是否使用KNN，需要根据具体问题的特点来决定：
- 数据量不是特别大
- 特征维度较低
- 样本分布比较均匀
- 对模型可解释性要求不高
在这些场景下，KNN往往能够提供不错的性能。