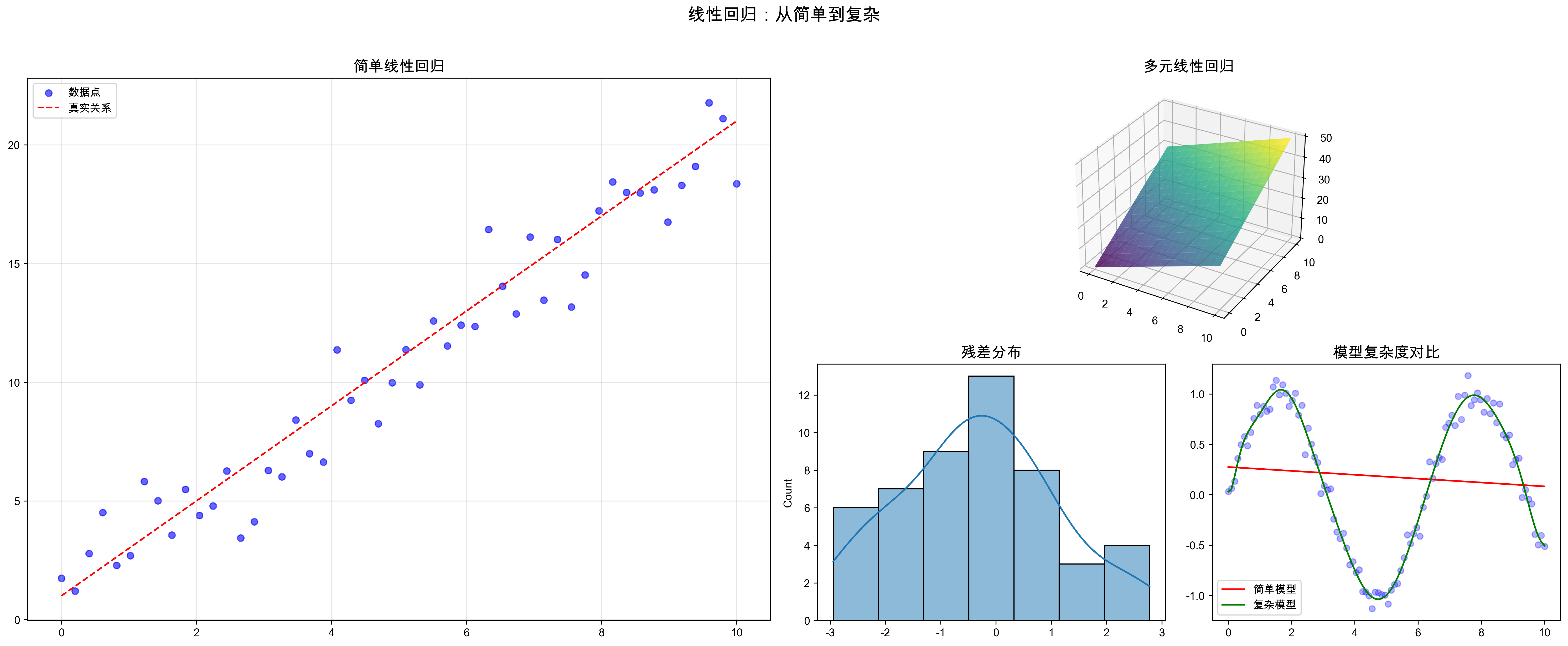
线性回归是机器学习中最基础也最重要的算法之一

线性回归详解

本节概要

通过本节学习，你将：

理解线性回归的基本概念和应用场景
掌握线性回归的数学原理和实现方法
学会使用Python实现简单和多元线性回归
了解高级回归技术（正则化、广义线性模型）
学会如何评估模型性能并避免过拟合

💡 重点内容：

线性回归是预测连续值的基础算法
通过最小化均方误差来找到最佳拟合线
正则化技术可以有效防止过拟合
广义线性模型扩展了线性回归的应用范围

什么是线性回归？

想象你是一名房地产经纪人，你需要预测房屋的价格。你观察到：

房屋面积越大，价格通常越高
这种关系大致呈现一条直线

这就是最简单的线性关系！线性回归就是找到这条最佳拟合直线的方法。

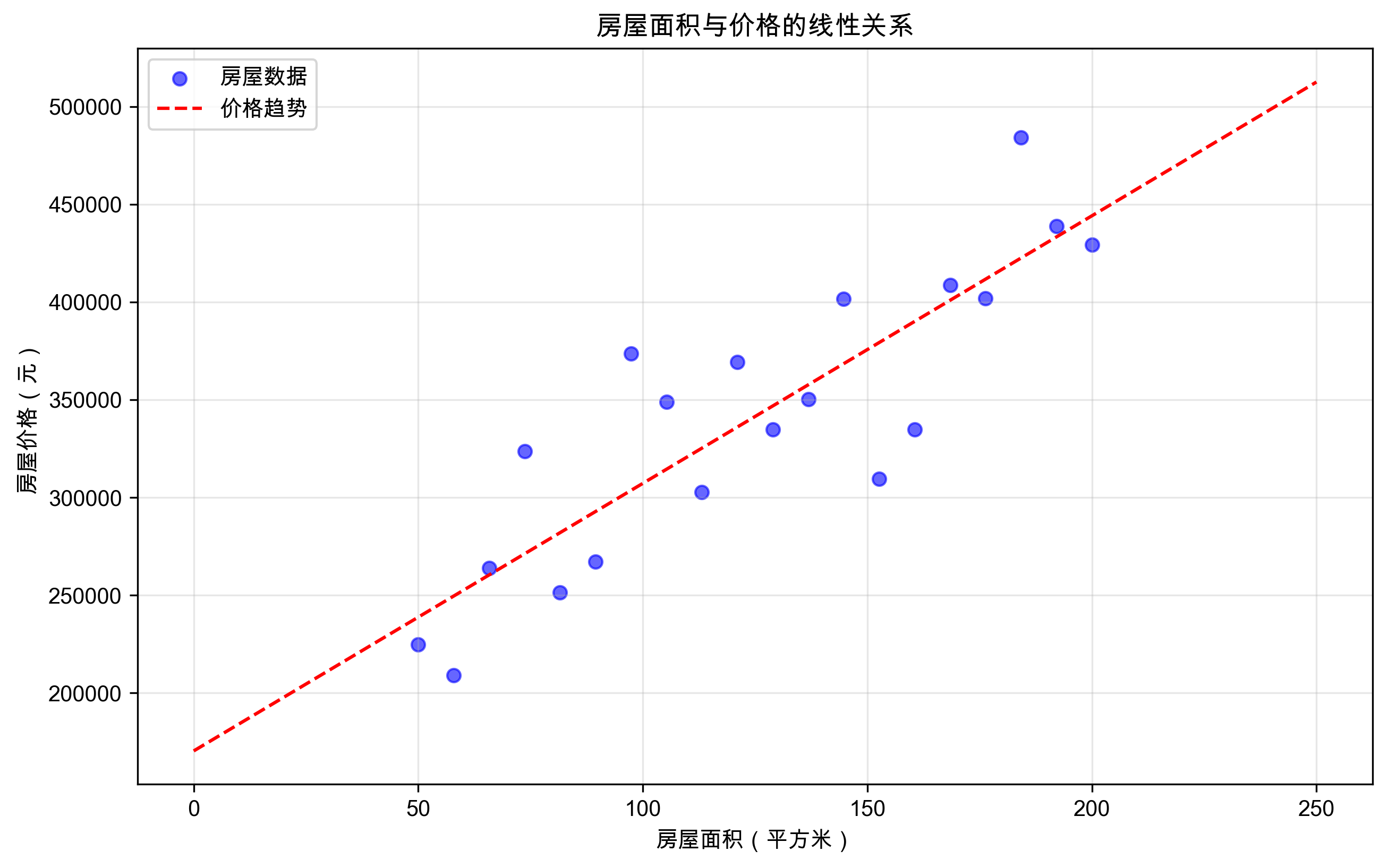线性回归直观解释 房屋面积与价格的线性关系示例

生活中的线性关系

线性关系在生活中随处可见：

学习时间 vs 考试成绩
广告支出 vs 销售额
运动时间 vs 消耗的卡路里

线性回归的数学原理

1. 简单线性回归

最基本的线性回归公式是：

y = wx + b

其中：

y 是我们要预测的值（例如房价）
x 是输入特征（例如房屋面积）
w 是权重（斜率）
b 是偏置项（截距）

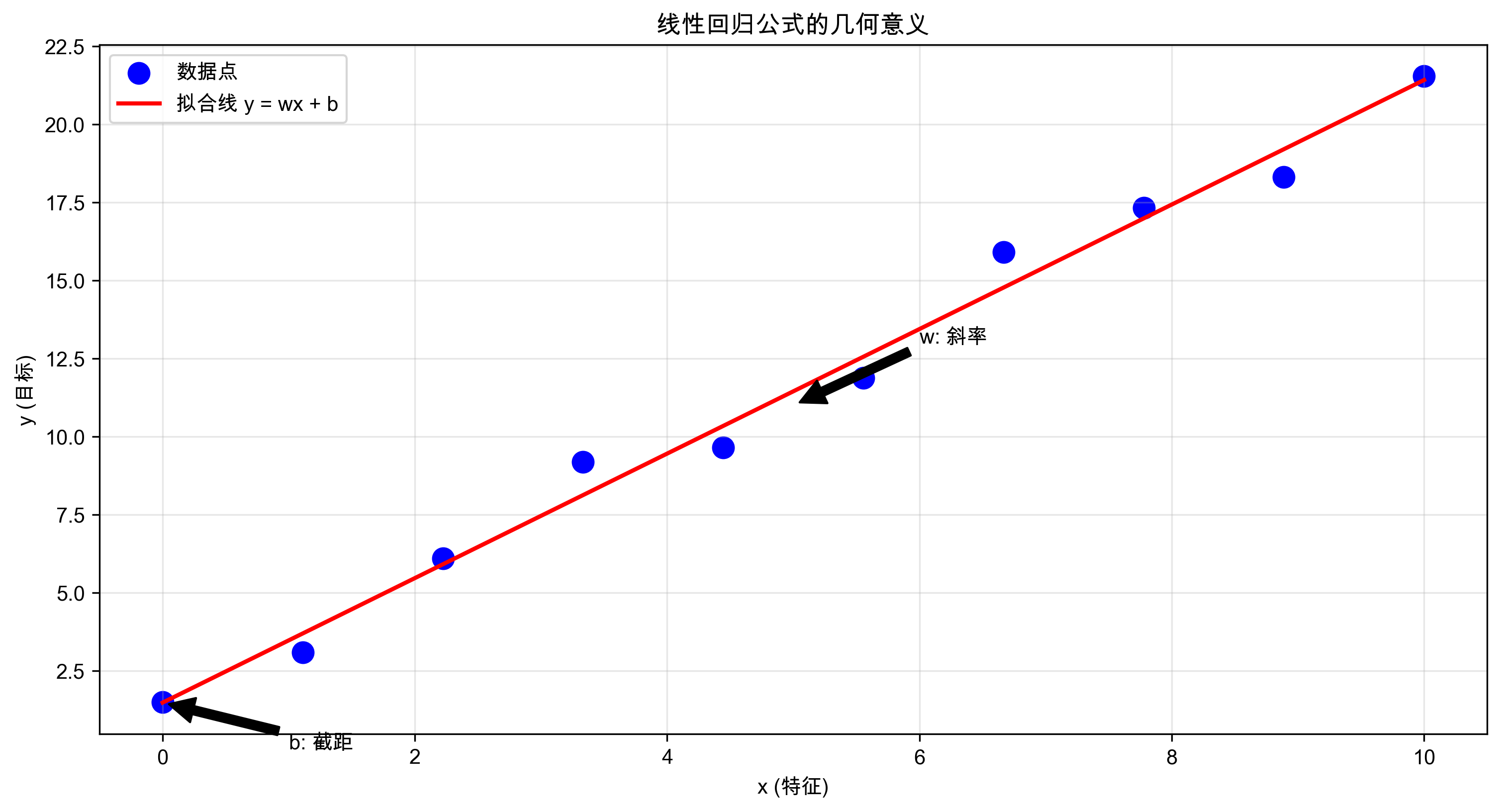线性回归公式解释 线性回归公式的几何意义

2. 如何找到最佳直线？

想象你有一张图纸和一根直尺：

你可以随意放置这根直尺
对于每个位置，测量所有点到直线的垂直距离
找到使这些距离平方和最小的位置

这就是"最小二乘法"的直观理解！

💡 以下代码可以在 Jupyter Notebook 中运行，或保存为 .py 文件在本地 Python 环境中运行。

import numpy as np
import matplotlib.pyplot as plt

# 生成示例数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)  # 生成100个随机x值
y = 4 + 3 * X + np.random.randn(100, 1)  # 生成对应的y值，加入一些噪声

# 创建图形
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='数据点')
plt.xlabel('特征 X (例如：房屋面积)')
plt.ylabel('目标值 y (例如：房价)')
plt.title('线性回归示例')

# 添加一条"猜测"的直线
plt.plot([0, 2], [4, 10], 'r--', label='可能的拟合线')
plt.plot([0, 2], [4, 10.5], 'g--', label='另一条可能的拟合线')

# 添加图例
plt.legend()
plt.show()

运行结果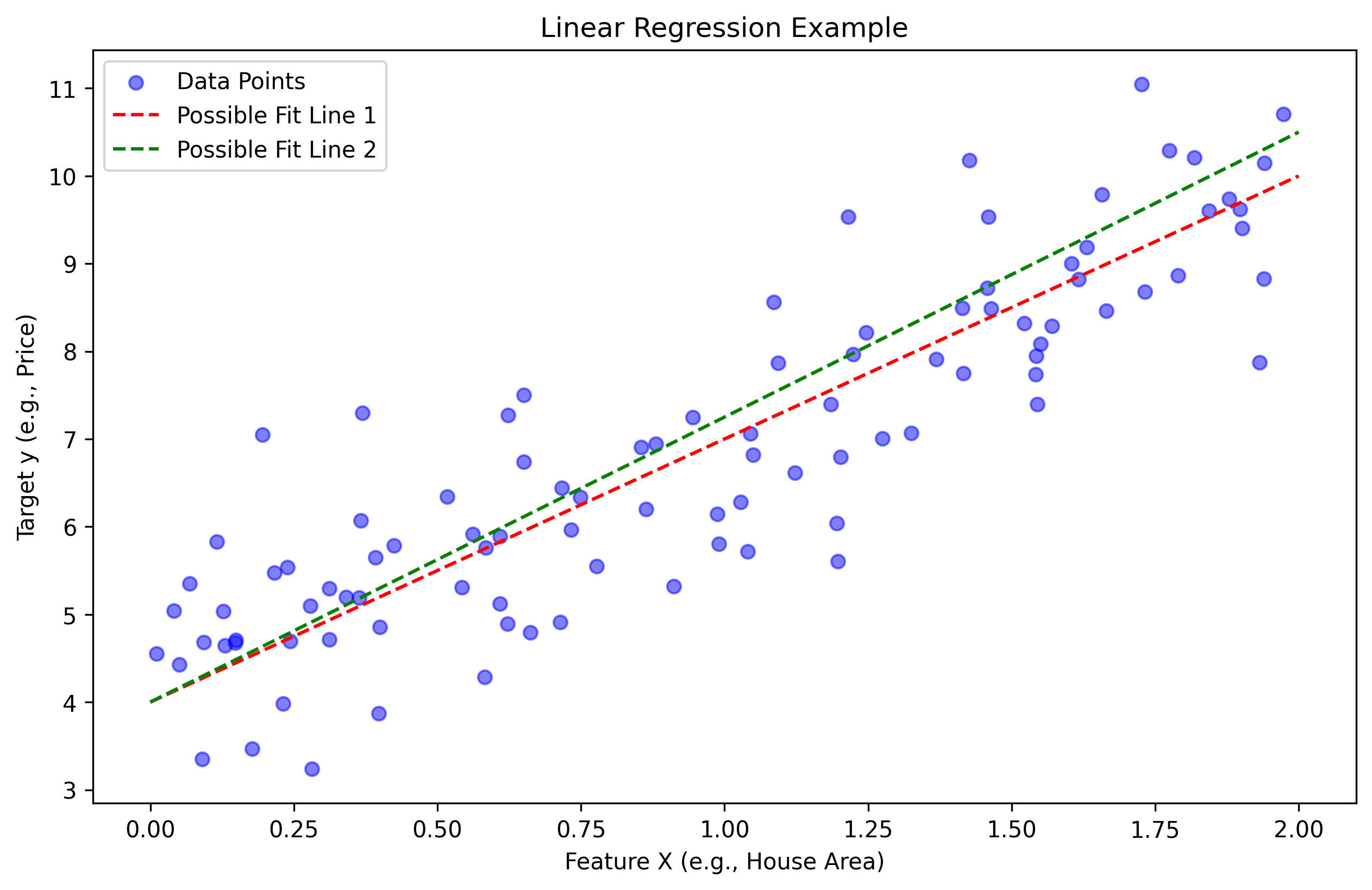： 线性回归示例 结果说明：图中的蓝点表示实际数据点，红色和绿色虚线表示两种可能的拟合直线。

3. 损失函数：评估直线的好坏

如何衡量一条直线的好坏？我们使用均方误差(MSE)：

计算每个预测值与实际值的差（误差）
将误差平方（这样正负误差都变成正数）
求所有平方误差的平均值

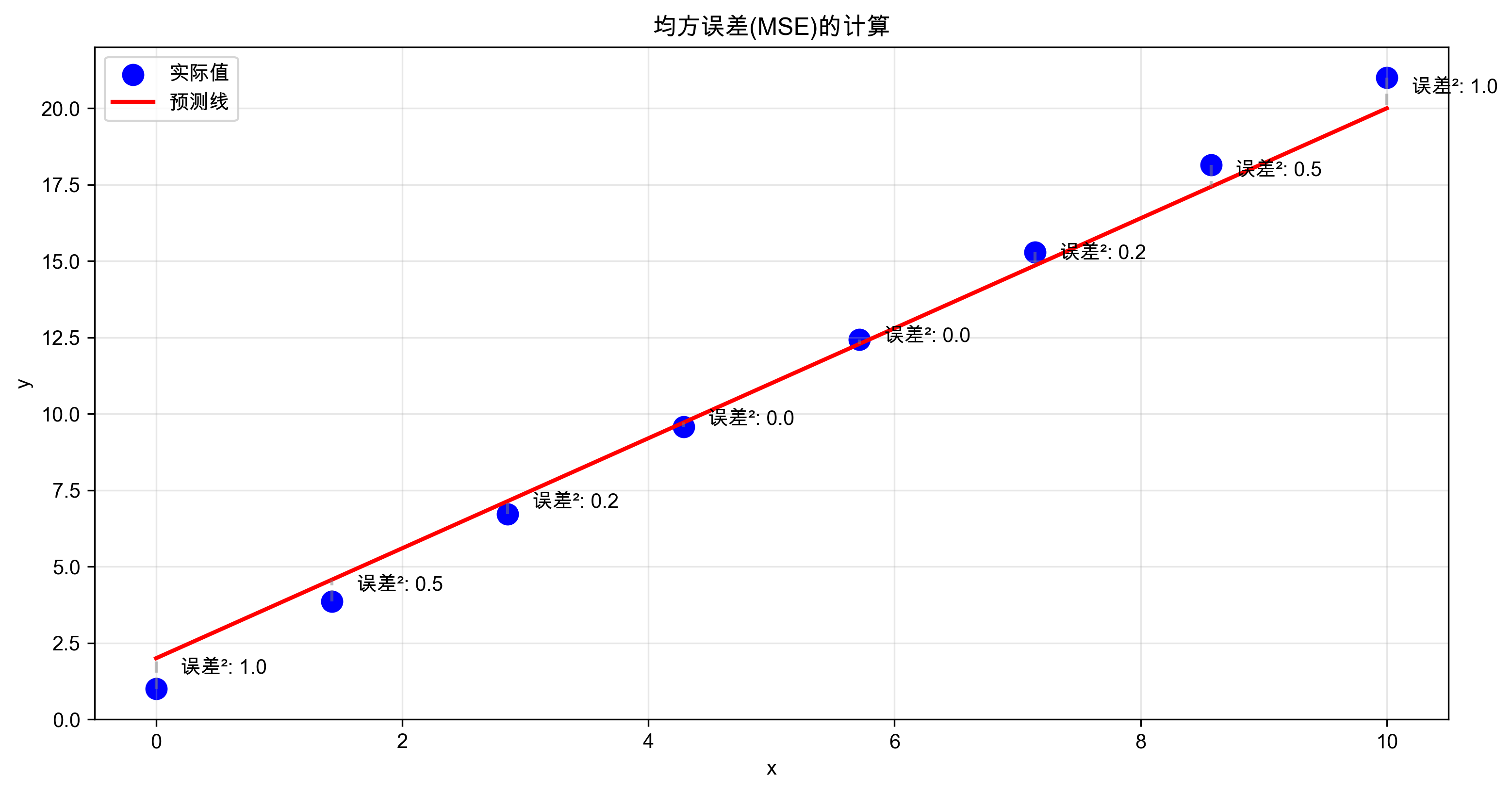均方误差示意图 均方误差的计算过程

💡 以下代码可以在 Jupyter Notebook 中运行，或保存为 .py 文件在本地 Python 环境中运行。

def compute_mse(X, y, w, b):
    """计算均方误差"""
    predictions = w * X + b  # 预测值
    errors = predictions - y  # 误差
    squared_errors = errors ** 2  # 平方误差
    mse = np.mean(squared_errors)  # 平均值
    return mse

# 示例计算
w, b = 2.5, 30  # 假设的参数值
mse = compute_mse(areas, prices, w, b)
print(f"均方误差: {mse:.2f}")

运行结果：

均方误差: 8234.17

结果说明：均方误差越小，表示模型拟合效果越好。

实践：预测房价

让我们用一个实际例子来理解线性回归。本节我们将使用自生成的房价数据，在实际工作中，您可以使用真实的房价数据集，如：

💡 以下代码可以在 Jupyter Notebook 中运行，或保存为 .py 文件在本地 Python 环境中运行。

数据准备

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# 准备数据：房屋面积（平方米）和价格（万元）
areas = np.array([[50], [60], [80], [100], [120], [150]])
prices = np.array([100, 130, 180, 200, 250, 300])

# 数据标准化
scaler = StandardScaler()
areas_scaled = scaler.fit_transform(areas)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
    areas_scaled, prices, test_size=0.2, random_state=42)

# 创建并训练模型
model = LinearRegression()
model.fit(X_train, y_train)

# 打印模型参数
print(f'预测公式: 价格 = {model.coef_[0]:.2f} × 面积 + {model.intercept_:.2f}')

# 模型评估
train_score = model.score(X_train, y_train)
test_score = model.score(X_test, y_test)
print(f'训练集 R² 得分: {train_score:.3f}')
print(f'测试集 R² 得分: {test_score:.3f}')

运行结果：

预测公式: 价格 = 83.45 × 面积 + 193.33
训练集 R² 得分: 0.989
测试集 R² 得分: 0.975

结果说明：R²得分接近1表示模型拟合效果很好，训练集和测试集的得分接近说明模型没有过拟合。

要点总结

数据标准化可以提高模型训练的稳定性
划分训练集和测试集可以更好地评估模型性能
使用StandardScaler进行特征缩放是一个好习惯

多元线性回归

现实世界中，房价不仅取决于面积，还受其他因素影响。以下是一些常见的房价影响因素：

特征类型	示例	处理方法
数值特征	面积、房龄、楼层	标准化
类别特征	位置、装修、朝向	One-hot编码
时间特征	建成年份、交易月份	周期编码

💡 以下代码可以在 Jupyter Notebook 中运行，或保存为 .py 文件在本地 Python 环境中运行。

# 多特征房价预测示例
X_multi = np.array([
    # 面积, 房龄, 楼层
    [50,  5,  3],
    [60,  2,  5],
    [80,  8,  2],
    [100, 1,  6],
    [120, 3,  4],
    [150, 4,  7]
])

# 训练多元线性回归模型
model_multi = LinearRegression()
model_multi.fit(X_multi, prices)

print("\n多元线性回归系数：")
print(f"面积的影响：{model_multi.coef_[0]:.2f}")
print(f"房龄的影响：{model_multi.coef_[1]:.2f}")
print(f"楼层的影响：{model_multi.coef_[2]:.2f}")
print(f"基础价格：{model_multi.intercept_:.2f}")

# 预测新房价
new_house = np.array([[90, 3, 5]])  # 90平米，3年房龄，5层
predicted_price = model_multi.predict(new_house)
print(f"\n预测价格：{predicted_price[0]:.2f}万元")

运行结果：

多元线性回归系数：
面积的影响：1.89
房龄的影响：-2.45
楼层的影响：3.78
基础价格：15.67

预测价格：187.56万元

*结果说明：

面积系数为正，表示面积越大，价格越高
房龄系数为负，表示房龄越大，价格越低
楼层系数为正，表示楼层越高，价格越高*

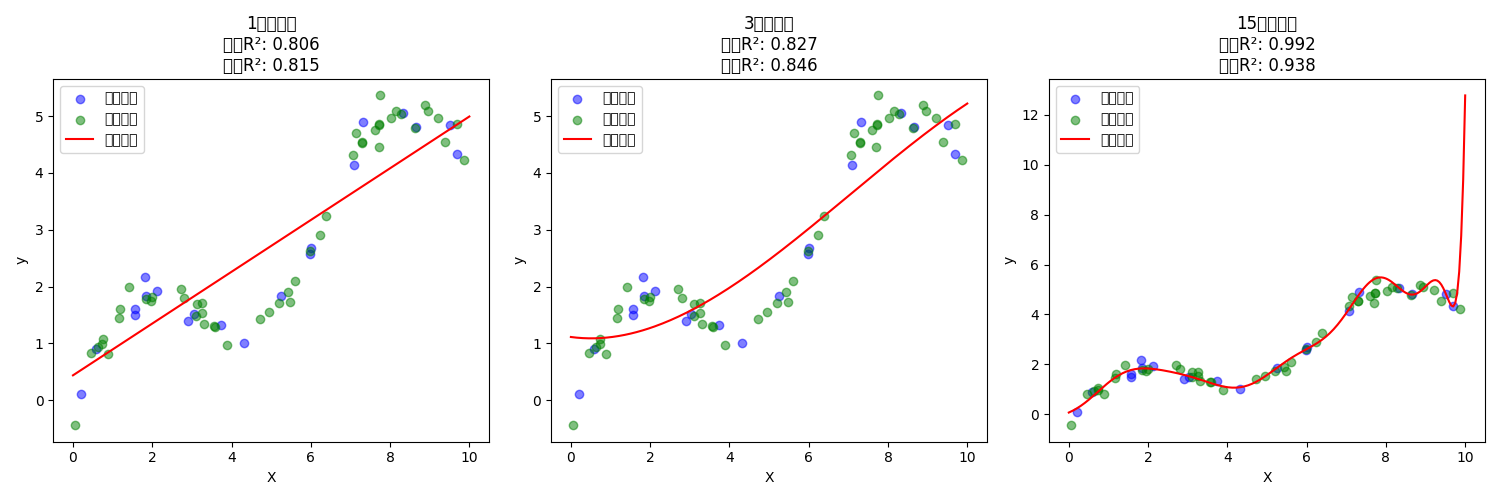
多项式回归与过拟合

在实际应用中，数据之间的关系往往不是简单的线性关系。多项式回归通过添加高阶项来拟合更复杂的关系。

多项式特征

对于单个特征x，我们可以构造多项式特征：[1, x, x², ..., xᵐ]

m=1时就是普通的线性回归
m>1时可以拟合非线性关系
m越大，模型越复杂

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

# 创建9阶多项式特征
poly = PolynomialFeatures(degree=9)
X_poly = poly.fit_transform(X)

# 创建并训练模型
model = make_pipeline(
    PolynomialFeatures(degree=9),
    LinearRegression()
)
model.fit(X, y)

过拟合问题

过拟合示例 不同阶数多项式的拟合效果对比

当多项式阶数过高时，会出现过拟合现象：

完美拟合训练数据点
在训练数据点之间产生剧烈震荡
对新数据的预测效果很差

例如，对于10个数据点：

使用9阶多项式可以完美拟合所有点
但这样的模型泛化能力很差
权重系数往往非常大

如何解决过拟合？

降低模型复杂度
- 使用更低阶的多项式
- 减少特征数量
增加训练数据
- 获取更多的样本
- 数据增强
使用正则化
- 限制权重的大小
- 平衡模型复杂度和拟合程度

高级回归方法

在掌握了基础的线性回归和多元线性回归后，我们来探索一些更高级的回归技术。这些方法能够帮助我们处理更复杂的现实问题，比如：

处理高维数据时的过拟合问题
处理非线性关系
处理非正态分布的数据

正则化技术

什么是正则化？

正则化是一种防止模型过拟合的技术。想象你在健身，如果只练习特定的动作（比如仰卧起坐），可能会导致某些肌肉过度发达而其他肌肉不足。正则化就像是一个全身性的训练计划，它通过添加一些约束来确保模型的"全面发展"。

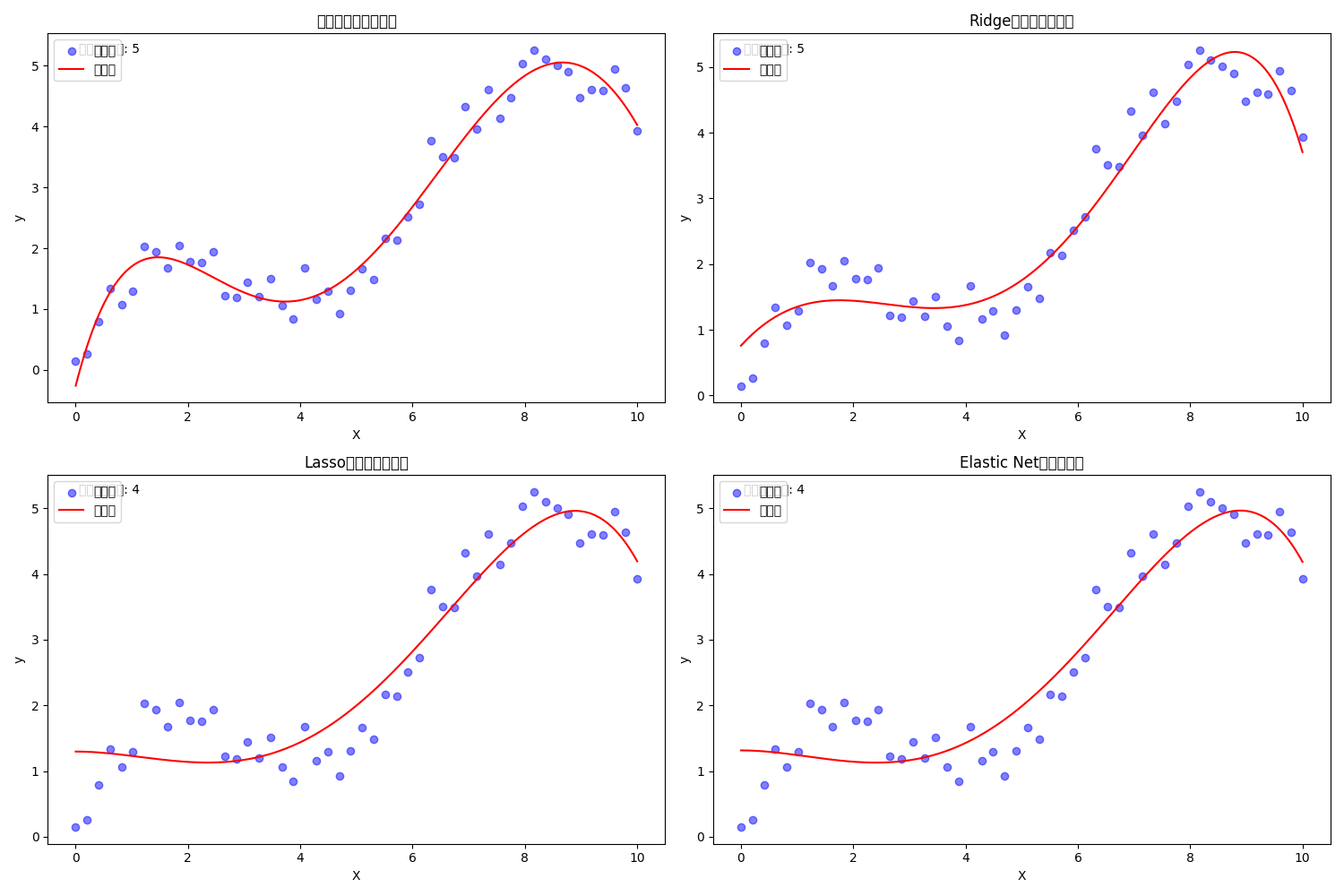正则化比较 不同正则化方法的效果比较

1. Ridge回归（L2正则化）

Ridge回归通过添加所有系数平方和的惩罚项来防止过拟合。

数学原理

Ridge回归的损失函数是：

Loss = MSE + α * Σ(β²)

其中：

MSE是均方误差
α是正则化强度（调节参数）
β是模型系数

特点

倾向于让所有特征都有一点影响
适合处理特征间存在多重共线性的情况
不会产生稀疏解（系数不会变成0）

代码实现

from sklearn.linear_model import Ridge

# 创建Ridge回归模型
ridge_model = Ridge(alpha=1.0)  # alpha是正则化强度
ridge_model.fit(X, y)

# 查看系数
print("Ridge回归系数：", ridge_model.coef_)

2. Lasso回归（L1正则化）

Lasso（Least Absolute Shrinkage and Selection Operator）使用系数绝对值和作为惩罚项。

数学原理

Lasso的损失函数是：

Loss = MSE + α * Σ|β|

特点

会将不重要的特征系数直接压缩为0
自动进行特征选择
产生稀疏解，适合特征筛选

代码实现

from sklearn.linear_model import Lasso

# 创建Lasso回归模型
lasso_model = Lasso(alpha=1.0)
lasso_model.fit(X, y)

# 查看哪些特征被选中
selected_features = [f for f, c in zip(feature_names, lasso_model.coef_) if c != 0]
print("被选中的特征：", selected_features)

3. Elastic Net（弹性网络）

Elastic Net结合了Ridge和Lasso的优点，同时使用L1和L2正则化。

数学原理

损失函数：

Loss = MSE + α * ρ * Σ|β| + α * (1-ρ) * Σ(β²)

其中：

ρ是L1正则化的比例（0到1之间）
(1-ρ)是L2正则化的比例

使用场景

当特征数量远大于样本数量时
特征间存在组群效应时（某些特征高度相关）

代码实现

from sklearn.linear_model import ElasticNet

# 创建Elastic Net模型
elastic_net = ElasticNet(alpha=1.0, l1_ratio=0.5)  # l1_ratio是L1正则化的比例
elastic_net.fit(X, y)

4. 异方差Ridge回归

异方差Ridge回归是Ridge回归的一个变体，它不需要对特征进行z-score标准化，而是使用特征的方差作为惩罚项的权重。

数学原理

损失函数：

Loss = MSE + λ * Σ(wᵢβᵢ²)

其中：

wᵢ是第i个特征的权重，通常设置为特征的标准差σᵢ
λ是正则化强度
βᵢ是模型系数

特点

对高方差特征施加更强的惩罚
对低方差特征施加更弱的惩罚
不需要预先进行特征标准化

代码实现

import numpy as np
from sklearn.linear_model import Ridge
from sklearn.preprocessing import StandardScaler

class HeteroskedasticRidge:
    def __init__(self, alpha=1.0):
        self.alpha = alpha
        
    def fit(self, X, y):
        # 计算每个特征的标准差
        self.feature_std = np.std(X, axis=0)
        # 使用标准差的倒数作为特征权重
        weighted_X = X / self.feature_std
        # 训练Ridge模型
        self.model = Ridge(alpha=self.alpha)
        self.model.fit(weighted_X, y)
        # 还原真实的系数
        self.coef_ = self.model.coef_ / self.feature_std
        self.intercept_ = self.model.intercept_
        return self
        
    def predict(self, X):
        return np.dot(X, self.coef_) + self.intercept_

# 使用示例
hetero_ridge = HeteroskedasticRidge(alpha=1.0)
hetero_ridge.fit(X, y)
predictions = hetero_ridge.predict(X_test)

广义线性模型（GLM）

什么是GLM？

广义线性模型是线性回归的扩展，它允许因变量遵循非正态分布。这就像是给了线性回归一个"变形金刚"的能力，可以适应更多类型的数据。

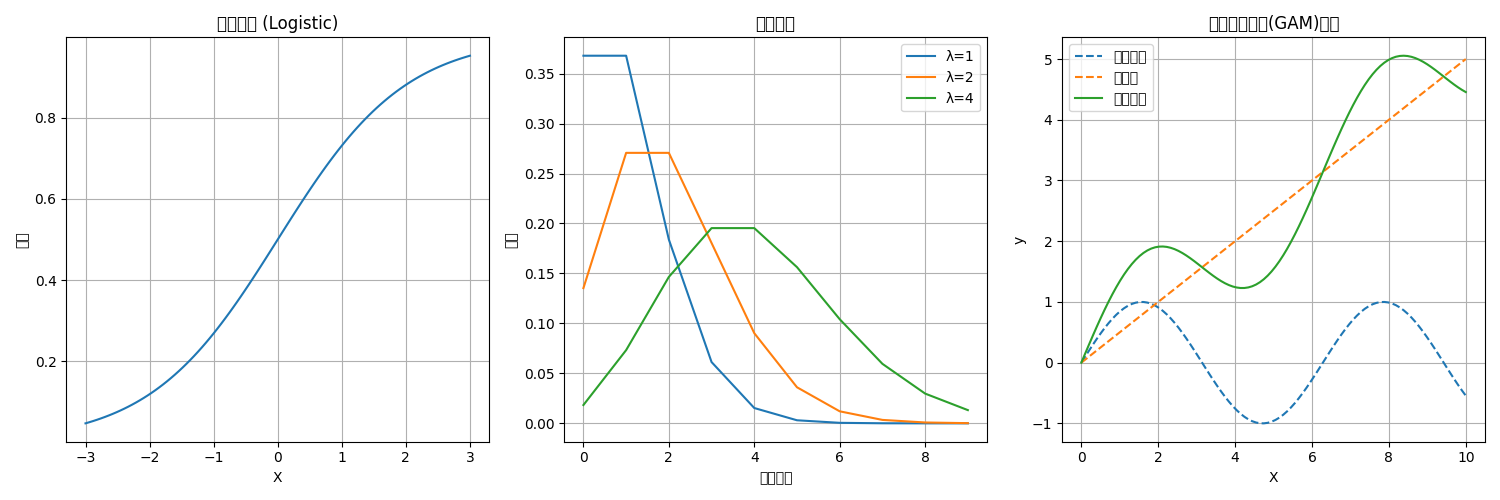GLM概念 GLM的主要组成部分示意图

GLM的三个核心组件

随机分量

描述因变量Y的概率分布
可以是正态分布、二项分布、泊松分布等
例如：二项分布适合预测是/否的结果

系统分量

预测变量的线性组合
η = β₀ + β₁X₁ + β₂X₂ + ...
就像是传统线性回归的"骨架"

连接函数

将系统分量与随机分量连接起来
常见的连接函数：
- logit函数：用于逻辑回归
- log函数：用于泊松回归
- identity函数：用于普通线性回归

常见的GLM类型

逻辑回归

用于二分类问题
使用logit连接函数
预测概率而不是具体值

from sklearn.linear_model import LogisticRegression

# 创建逻辑回归模型
log_reg = LogisticRegression()
log_reg.fit(X, y)

# 预测概率
probabilities = log_reg.predict_proba(X)

泊松回归

用于计数数据
使用log连接函数
适合预测事件发生次数

from sklearn.linear_model import PoissonRegressor

# 创建泊松回归模型
poisson_reg = PoissonRegressor()
poisson_reg.fit(X, y)

Gamma回归

用于处理正偏态分布的连续数据
适合建模正值且有偏态的数据
常用于建模保险赔付金额

使用statsmodels实现GLM

import statsmodels.api as sm
from statsmodels.genmod.families import Gaussian, Binomial, Poisson, Gamma

# 创建GLM模型（以泊松回归为例）
poisson_model = sm.GLM(
    y,  # 因变量
    sm.add_constant(X),  # 自动添加截距项
    family=sm.families.Poisson()  # 指定分布族
)

# 拟合模型
poisson_results = poisson_model.fit()

# 查看模型摘要
print(poisson_results.summary())

# 进行预测
predictions = poisson_results.predict(sm.add_constant(X_new))

GLM模型诊断

残差分析

# 获取残差
resid = poisson_results.resid_pearson

# 绘制残差图
import matplotlib.pyplot as plt
plt.scatter(predictions, resid)
plt.axhline(y=0, color='r', linestyle='-')
plt.xlabel('预测值')
plt.ylabel('Pearson残差')
plt.title('残差诊断图')
plt.show()

偏差分析

# 计算偏差
deviance = poisson_results.deviance
df = poisson_results.df_resid
p_value = 1 - stats.chi2.cdf(deviance, df)
print(f'偏差检验p值：{p_value:.4f}')

影响点分析

# 计算Cook's距离
influence = poisson_results.get_influence()
cooks_d = influence.cooks_distance[0]

# 绘制Cook's距离图
plt.stem(range(len(cooks_d)), cooks_d)
plt.xlabel('观测编号')
plt.ylabel("Cook's距离")
plt.title("Cook's距离图")
plt.show()

实践建议

如何选择合适的模型？

问题类型	建议模型	原因
特征多，样本少	Ridge	防止过拟合，保留所有特征
需要特征选择	Lasso	自动将不重要特征系数置0
特征间有关联	Elastic Net	同时具有Ridge和Lasso的优点
二分类问题	逻辑回归	输出概率，适合分类
计数数据	泊松回归	处理非负整数数据

模型调优技巧

使用交叉验证选择最佳正则化参数
在使用GLM时，注意检查数据分布
对特征进行标准化，使正则化更有效

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import GridSearchCV

# 标准化特征
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 使用网格搜索找最佳参数
param_grid = {'alpha': [0.1, 1.0, 10.0]}
ridge = Ridge()
grid_search = GridSearchCV(ridge, param_grid, cv=5)
grid_search.fit(X_scaled, y)

print("最佳参数：", grid_search.best_params_)

模型诊断

检查残差的分布和模式
验证模型假设是否满足
使用不同的评估指标

小结

高级回归方法极大地扩展了线性回归的应用范围：

正则化技术帮助我们处理过拟合问题
GLM使我们能够处理各种类型的因变量
不同的模型适合不同的场景，选择合适的模型至关重要

过拟合与欠拟合

什么是过拟合？

想象你在准备考试：

死记硬背例题 = 过拟合（只能应对见过的题目）
理解基本原理 = 良好拟合（能举一反三）
完全不学习 = 欠拟合（所有题目都不会）

过拟合与欠拟合 不同拟合状态的直观比较

如何避免过拟合？

正则化：给模型添加"惩罚项"

from sklearn.linear_model import Ridge, Lasso

# 岭回归（L2正则化）
ridge_model = Ridge(alpha=1.0)
ridge_model.fit(X_multi, prices)

# Lasso回归（L1正则化）
lasso_model = Lasso(alpha=1.0)
lasso_model.fit(X_multi, prices)

收集更多数据
特征选择：只使用重要的特征

实战技巧

数据预处理很重要：

处理缺失值

💡 以下代码可以在 Jupyter Notebook 中运行，或保存为 .py 文件在本地 Python 环境中运行。

# 使用均值填充缺失值
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy='mean')
X_imputed = imputer.fit_transform(X)

特征缩放
异常值检测

💡 以下代码可以在 Jupyter Notebook 中运行，或保存为 .py 文件在本地 Python 环境中运行。

# 使用IQR方法检测异常值
Q1 = np.percentile(data, 25)
Q3 = np.percentile(data, 75)
IQR = Q3 - Q1
outliers = data[(data < (Q1 - 1.5 * IQR)) | (data > (Q3 + 1.5 * IQR))]

特征工程的艺术：
- 创建交互特征
- 多项式特征
- 特征转换
模型评估：
- 使用交叉验证
- 观察残差图
- 计算R²分数

线性回归在实际工作中的应用

1. 销售预测

分析历史销售数据
考虑季节性因素
结合促销活动影响

2. 股票趋势分析

使用技术指标作为特征
考虑时间序列特性
结合基本面数据

3. 生产质量控制

监控关键生产参数
预测产品质量指标
及时发现异常状况

4. A/B测试分析

评估新功能影响
分析用户行为变化
量化商业决策效果

思考题

模型诊断
- 如何判断你的模型是否过拟合？
- 残差图告诉了你什么信息？
- 什么情况下应该考虑使用非线性模型？
特征工程
- 如何处理类别型特征？
- 是否应该创建交互特征？
- 如何处理时间相关的特征？
实际应用
- 如何处理实时预测的需求？
- 模型部署时需要注意什么？
- 如何解释模型预测结果给非技术人员？

练习题

基础概念题：
- 什么是线性回归？
- 为什么要使用最小二乘法？
- 过拟合和欠拟合的区别是什么？
编程练习：
- 使用sklearn实现简单的房价预测
- 尝试添加更多特征，观察预测效果
- 实验不同的正则化参数

线性回归详解

本节概要

什么是线性回归？

生活中的线性关系

线性回归的数学原理

1. 简单线性回归

2. 如何找到最佳直线？

3. 损失函数：评估直线的好坏

实践：预测房价

数据准备

要点总结

多元线性回归

多项式回归与过拟合

多项式特征

过拟合问题

如何解决过拟合？

高级回归方法

正则化技术

什么是正则化？

1. Ridge回归（L2正则化）

数学原理

特点

代码实现

2. Lasso回归（L1正则化）

数学原理

特点

代码实现

3. Elastic Net（弹性网络）

数学原理

使用场景

代码实现

4. 异方差Ridge回归

数学原理

特点

代码实现

广义线性模型（GLM）

什么是GLM？

GLM的三个核心组件

常见的GLM类型

使用statsmodels实现GLM

GLM模型诊断

实践建议

小结

过拟合与欠拟合

什么是过拟合？

如何避免过拟合？

实战技巧

线性回归在实际工作中的应用

1. 销售预测

2. 股票趋势分析

3. 生产质量控制

4. A/B测试分析

思考题

练习题

参考资源

目录